Hi, I'm Martin!
Welcome to my website and online resume.
About me

I am an associate professor at the Niels Bohr Institute and the Niels Bohr International Academy at the University of Copenhagen, Denmark. My main research interests are in the interface between physics, mathematics, condensed and soft matter materials science, computer science, and biophysics. I live in Lund, Sweden, with my wife, Namsoon, who is an assistant professor at Lund University.
A large part of my research revolves around applications of geometry, topology, and combinatorial group theory to characterize and investigate materials and their properties. I am particularly interested in the emergence of hyperbolic geometry in biological and soft matter systems but apply these ideas and theories in a number of different settings as well. Furthermore, my Ph.D. studies revolved around the statistics and theory of scattering physics, and I am still active in the scattering physics communities as well.
Please download my resume, list of peer-reviewed publications, and teaching portfolio below: Resume List of publications Teaching portfolio
Research highlights

Active Particles Knead Three-Dimensional Gels into Porous Structures
The paper demonstrates how doping of active particles alters the topology of a colloidal gel system. We show this by deploying Topological Data Analysis (TDA) - or rather Persistent Homology - in concert with molecular dynamics simulations to investigate time series of emerging gel structures.
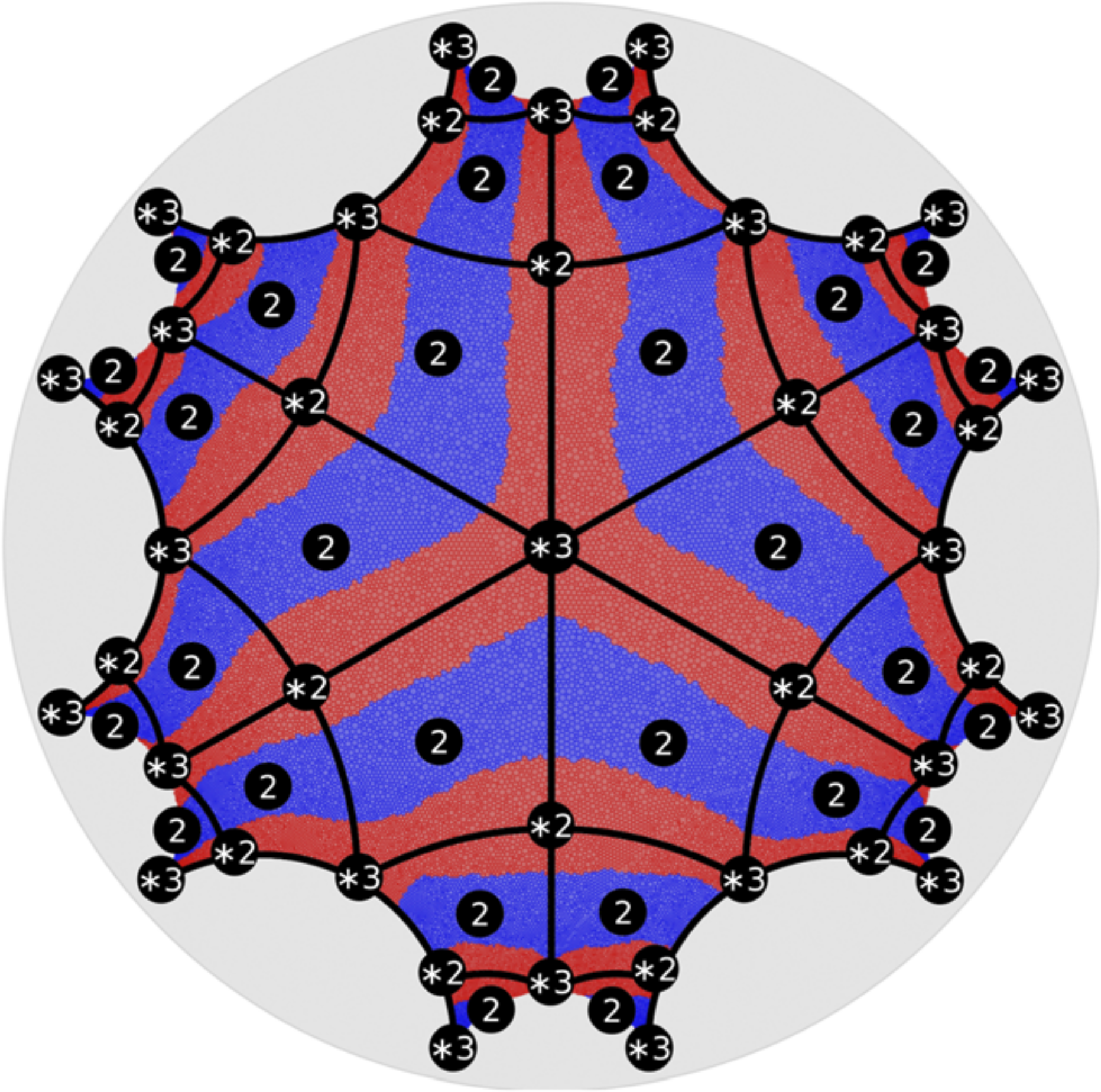
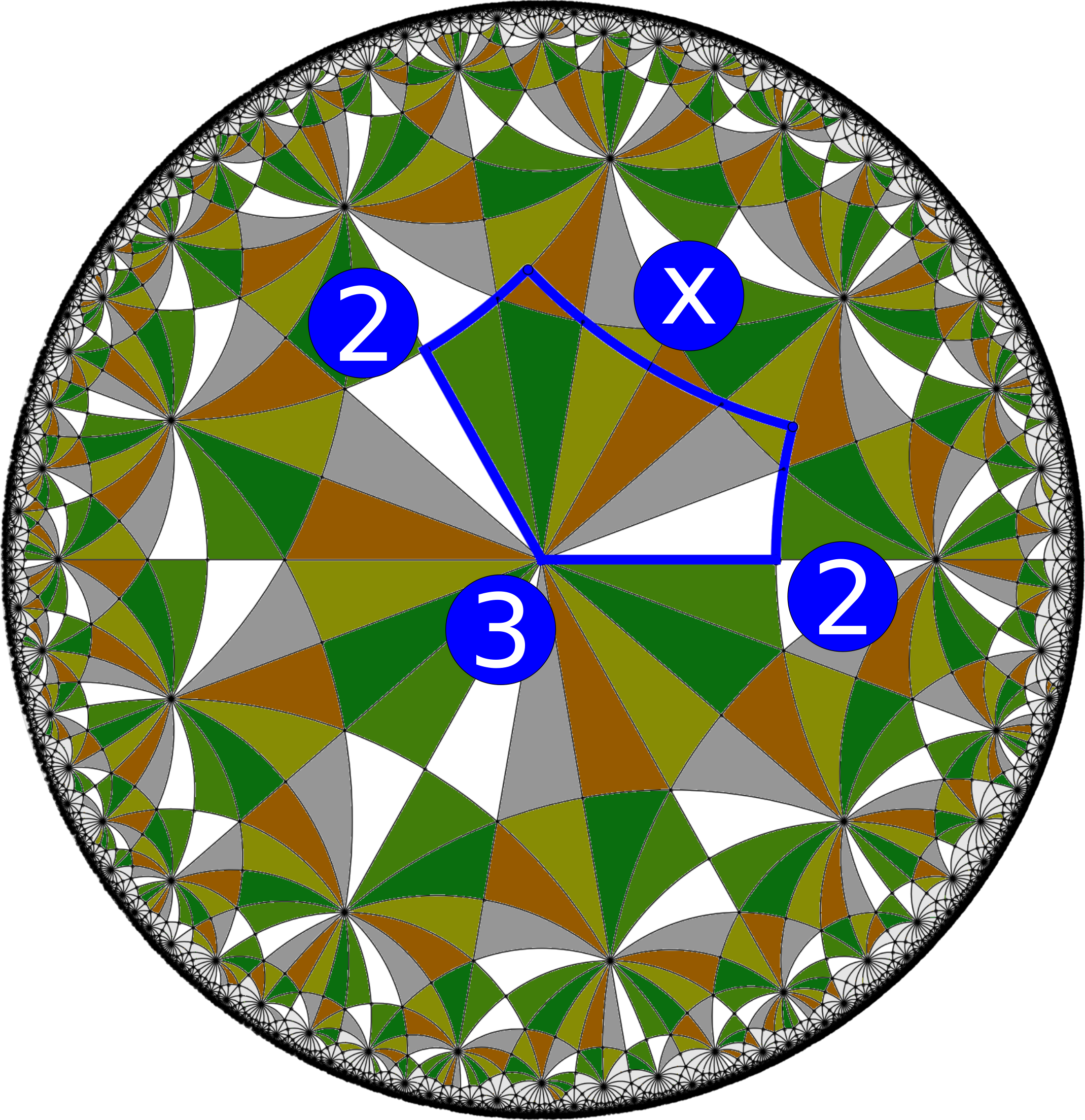
Mapping hyperbolic order in curved materials
We present a new method for visualisation and analysis of patterns on triply periodic negatively curved surfaces by mapping to two-dimensional hyperbolic space analogous to spherical projections in cartography thus effectively creating a more accessible “hyperbolic map” of the pattern.

The intrinsic group–subgroup structures of the Diamond and Gyroid minimal surfaces in their conventional unit cells
Using the software package GAP, we establish the crystallography for two periodic minimal surfaces in their conventional unit cells. We publish tables and information on each of the permitted symmetry groups on these surfaces, which can be found in the associated online repository.
Schwarzite nets: a wealth of 3-valent examples sharing similar topologies and symmetries
Schwarzites are carbon allotropes on surfaces of negative curvature; they are hyperbolic analogues to graphene making them very interesting from a materials science point of view. In this manuscript, we establish the most symmetric embeddings of Schwarzites on triply-periodic minimal surfaces. These are systematically enumerated and their structural properties evaluated; the manuscript also contains a large database of crystallographic information on these nets.
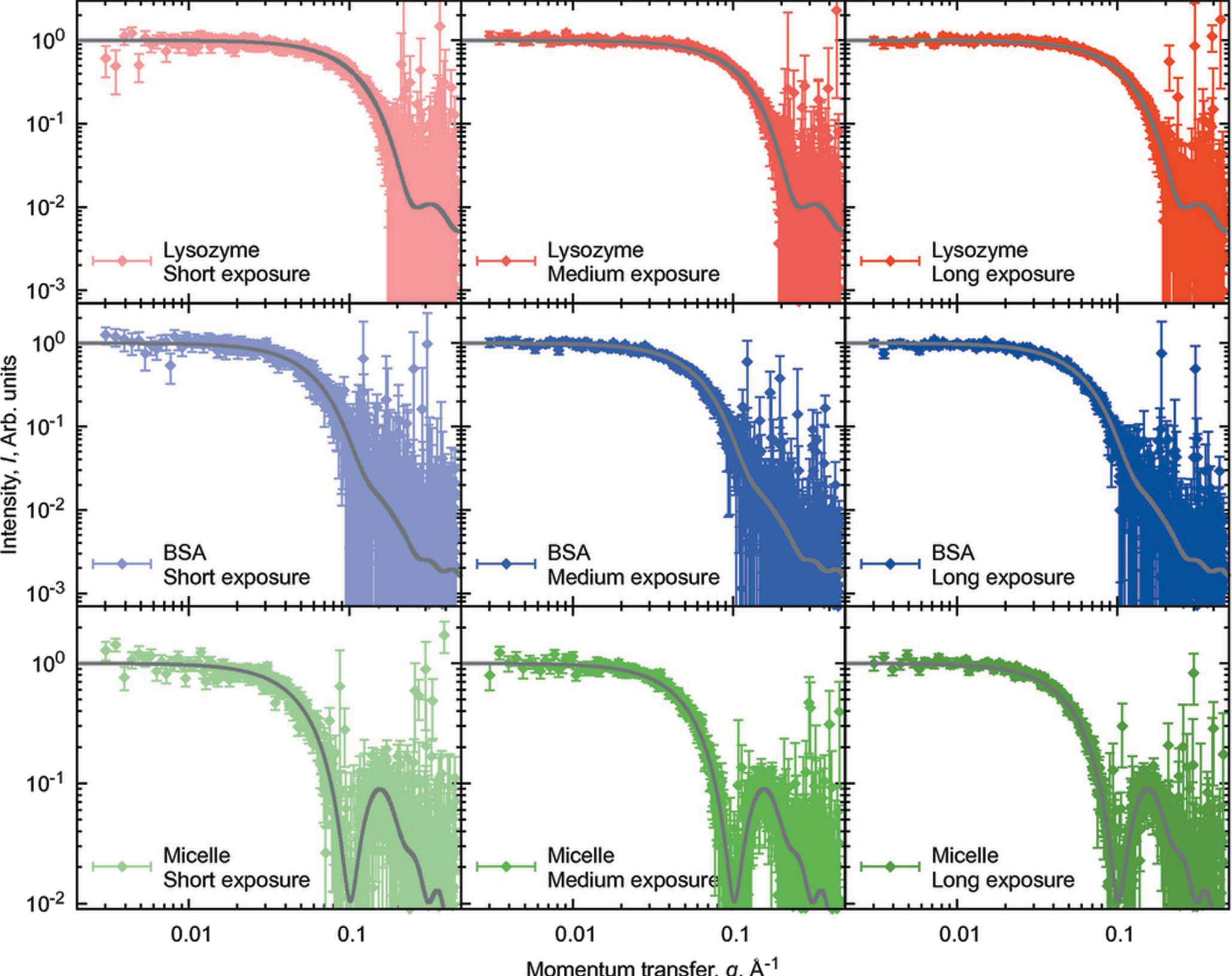
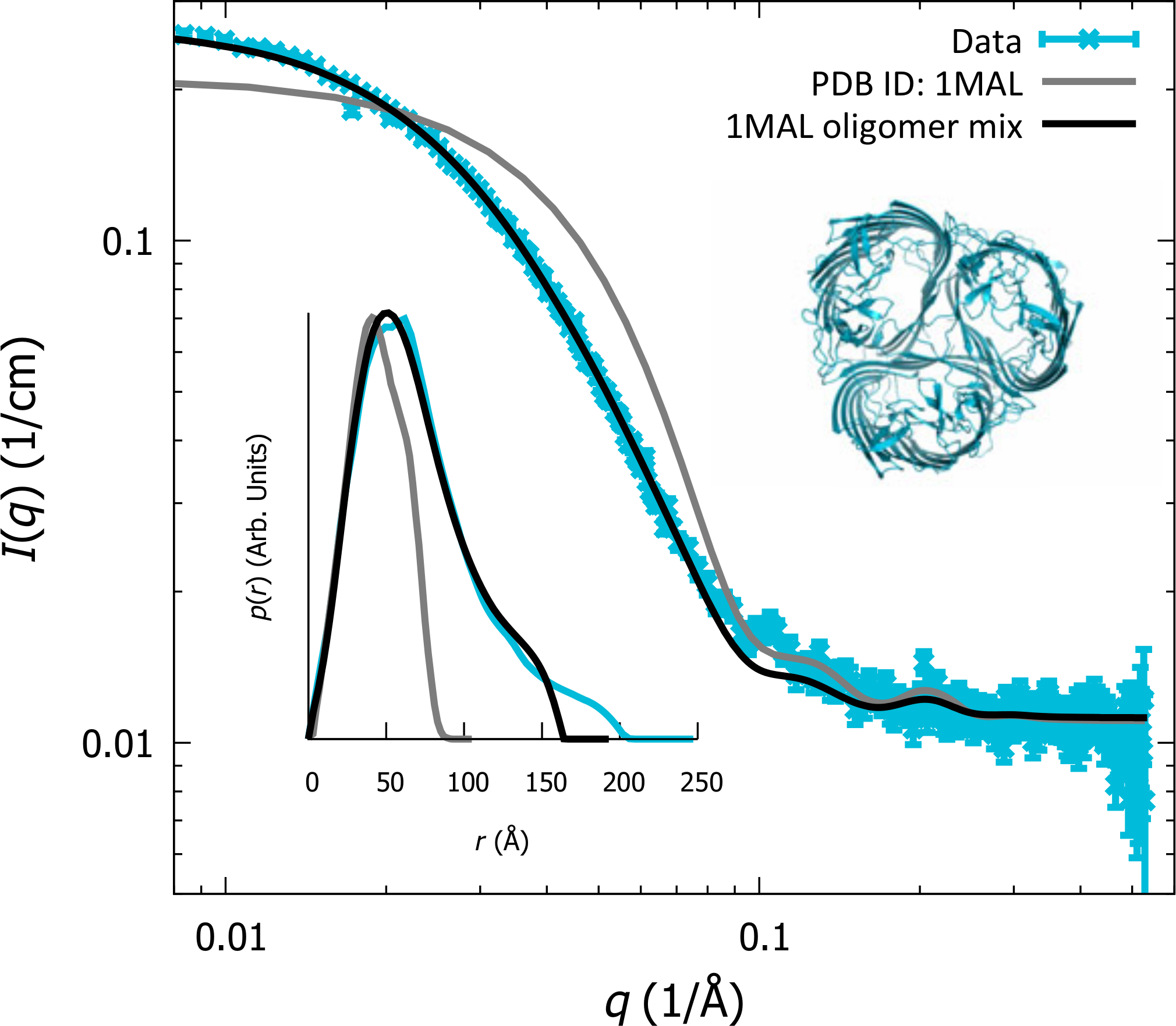
Experimental noise in small-angle scattering can be assessed using the Bayesian indirect Fourier transformation
My collaborator and I use ray-tracing simulation combined with the Bayesian Indirect Fourier Transformation (BIFT) to demonstrate, how the noise level in a given SAXS or SANS dataset is well estimated by the BIFT algorithm.
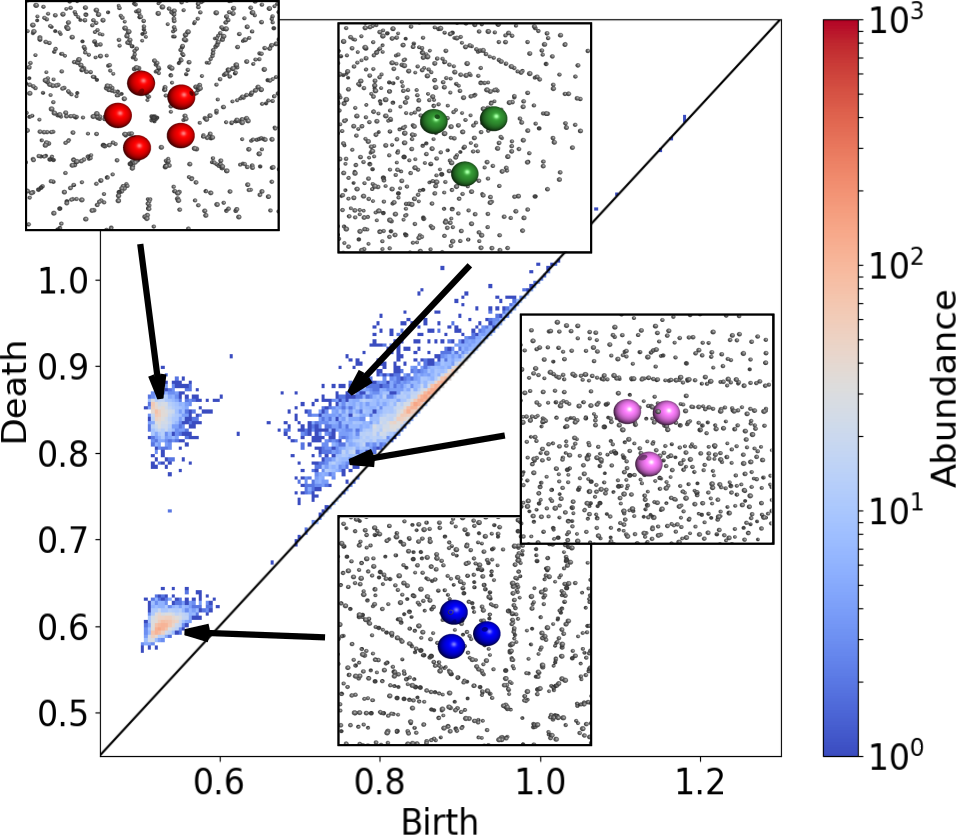
Evolution of local motifs and topological proximity in self-assembled quasi-crystalline phases
Using topological data analysis (persistent homology), my collaborators and I investigate the self-assembly of a colloidal system of particular interest due to its ability to form crystalline, quasicrystalline, and disordered phases with only minor tweaks to the interaction scheme. We demonstrate, how persistent homology allows us to efficiently probe and describe the emerging geometries in the system.
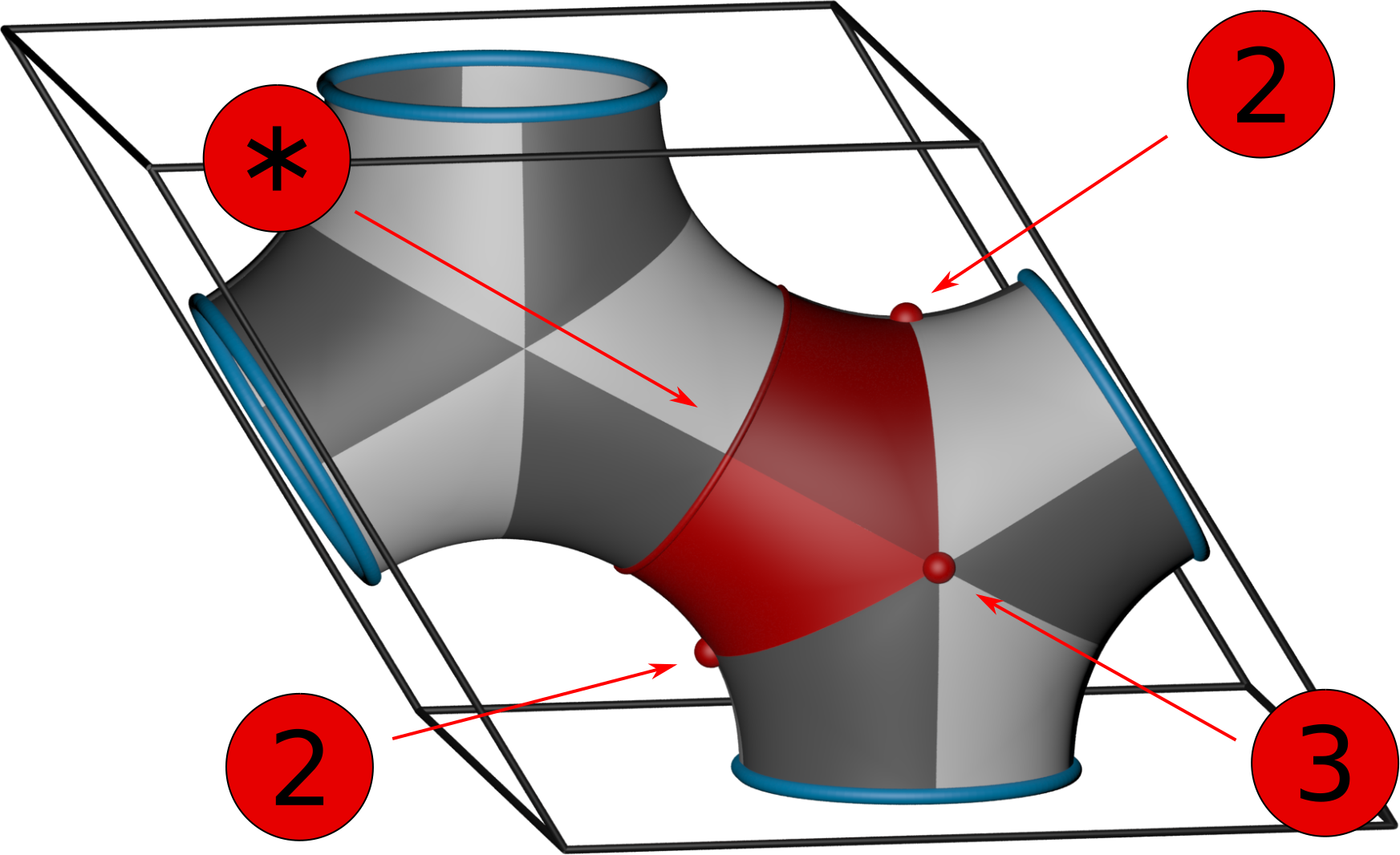
Polyhedra and packings from hyperbolic honeycombs
Through elaborate considerations of the hyperbolic crystallography of three periodic minimal surfaces, we describe the most symmetric embeddeds of distortions of the regular [3, N] honeycombs. In the process, we discover a number of novel reticular nets and infinite deltahedra. The presented methods are generally applicable and can be used to generate a suite of highly symmetric nets.
Have a look at my profiles at: Niels Bohr Institute Niels Bohr International Academy Google Scholar
Or find some of my work deposited in online databases at: EPINET RCSR
Teaching and projects
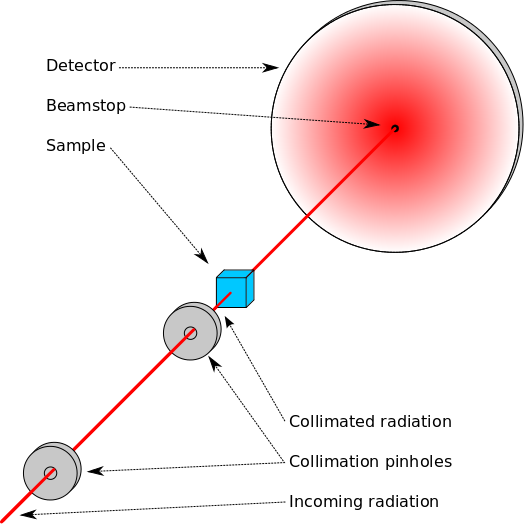
Ph.D.-school: Small-angle scattering: Principles, data analysis and advanced modeling
With a rotating roster of national and international experts, my colleagues and I organize a series of Ph.D. schools focusing on various aspects of small-angle scattering with a particular focus on data scientific aspects of small-angle scattering data analysis. The school specifically aims to be a very hands-on and practical course, and aims to introduce the students to the most prevalent and important methods used in the small-angle scattering community.

Ph.D.-school: Geometry and topology in contemporary materials science
Alongside colleagues from Australia and Germany, I am organizing the 4th edition of this Ph.D. school taking place in Copenhagen in the summer of 2026. This course will explore the geometry and topology of ordered cellular patterns such as foams, bicontinuous and polycontinuous forms and nets found in synthetic and biological materials, including: mesoporous silicates, metal organic frameworks and coordination polymers, amphiphiles, lipids, star polyphiles forming lyotropic liquid crystals block copolymers including star miktoarm copolymers.